みなさんこんにちは、ひでえぬです。
今回は、「プット・コール・パリティ」に関する問題です。
(この記事は、2023.4.16に加筆修正しました。)
「プット・コール・パリティ」について
「プット・コール・パリティ」というのは、ざっくりいうと「プットとコールのオプションは本質的には等価なので、一定の関係式が成り立つ」ということです。
今回のお話は、どちらかというと、実務に役立つというより、「CFP資格審査試験」の受験テクニックに近いものになると思います。
では、例題を見てみましょう。
(例題)
日経平均株価(日経225)が30,000円であるとき、次のうちオプション価格が最も高いのはどれか。
なお、満期は146日後、短期金利は0.01%であるとし、権利行使価格が同じコールオプションとプットオプションの間には、下の関係式が成立するものとする。
(解説)
突然ですが、
ここでオプションプレミアムトーナメントを行います。
上の1から4までの間で勝ち抜き戦を行い、優勝した選択肢が正解です。
組み合わせは私が決めさせていただきます。
勝ち抜き戦と言っても、4つしかないので、いきなり準決勝からです。
準決勝第1戦
準決勝第1戦はコールオプション同士の対戦です。
1 31,000円のコールオプション VS. 2 30,000円のコールオプション
ここで、前回のお話が生きてきます。
といっても、一月近く前の話ですが。
コールオプションは、権利行使価格が安い方が価値が高いので、2が決勝進出です。
準決勝第2戦
かたや準決勝第2戦はプットオプション同士の対戦です。
3 30,000円のプットオプション VS. 4 29,000円のプットオプション
こちらも、前回の内容を踏まえて考えると、プットオプションについては、権利行使価格が高い方が高く売れるので、価値が高いです。
よって、3が決勝進出となります。
決勝戦
2 30,000円のコールオプション VS. 3 30,000円のプットオプション
さて、決勝戦は同額のコールオプションとプットオプションの対決となりました。
コールオプションとプットオプションはどうやって比較したらよいのでしょうか。
ここで、問題文の関係式が出てきます。
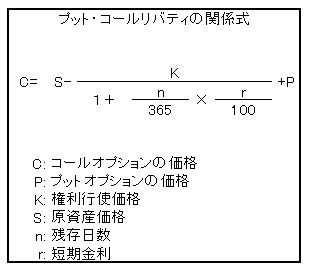
数字を入れてみるとこうなります。

ではここで、この式を計算・・・・しません
しなくても答えは出るからです。
分数の部分に着目しましょう。
これは「権利行使価格の現在価値」を表します。
上の式に関して言えば、金利がマイナスにならない限り、分母は1よりも大きくなります*1ので、分数部分は30,000円を下回ります。(もしかしてかなり僅かかもしれませんが・・・)
したがって、「30,000-分数部分」は必ずプラスになります。
どんなにわずかになっても、分数部分が30,000円を上回ることはありません。
したがって、「30,000-分数部分」を●とすると、上の式は、
C=●+P
(●>0)
と言い換えることができます。
つまり、C>P となりますので、
権利行使価格が30,000円のとき、コールオプションの方がプットオプションよりも高い
ことがわかります。
よって、
2が優勝!

ということになりますね。
(まとめ)
ここでわかることは、
例題のような問題の場合、決勝戦は「同じ金額(おそらく原資産価格)のコールオプションとプットオプションの対決」になる可能性がかなり高い
ということです。
仮に決勝戦がそうならなくても、準決勝のどちらかがこの対決になると思います。
また、「もっともオプションプレミアムが低いものはどれか」という問題もあり得ますが、解き方は同じです。
このように、解き方がわかっていれば、時間を節約できることもあるので、知っているとお得ですね。