みなさんこんにちは、ひでえぬです。
今日は資本資産価格決定モデル(CAPM)に関するおはなしです。
ちなみにCAPMは
きゃっぷえむ
と読むっていうことを、DVDを聴いていて初めて知りました。
(しーえーぴーえむだと思っていました)
文字情報だけだと意外とわからないものですね。
下のようなグラフが出てきます。
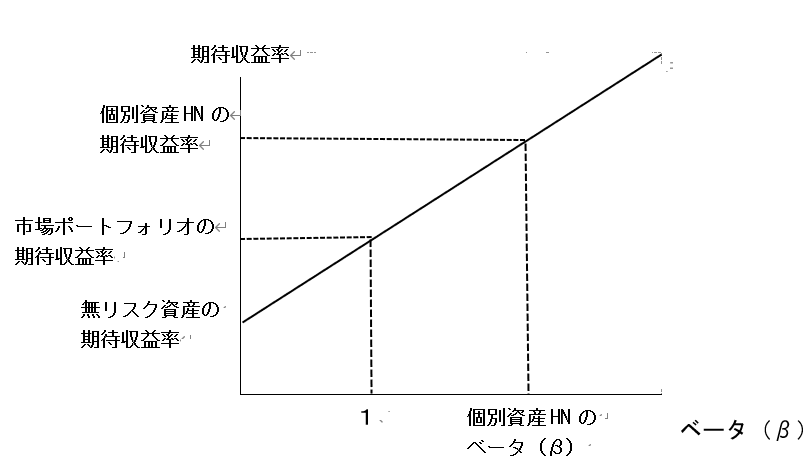
無リスク資産(元本割れしない資産、例えば定期預金など)とリスク資産(無リスク資産以外のもの、例えば株式や投資信託、などなど)を組み合わせて運用した場合の期待収益率(リターン)とリスクの関係をグラフにあらわしたものです。
縦軸に期待収益率、横軸にリスク指標としてベータ(β)をとると、上のようになります。
ベータといえばこれですね。

(ソニーHPより)
違います。
ベータ(Beta)とは、CAPMにおける資産のリスクの尺度であり、マーケットポートフォリオの変動に対して、資産のリターンがどれだけ連動して動くかを示したものである。
要するにベータというのは、市場の価格変動に対して資産がどれだけ反応するかを示した数値といえます。
無リスク資産は0ですし、市場ポートフォリオは1になります。この両者を結んだ直線を
証券市場線
といいます。
似たようなもので、リスク指標についてベータではなくVHS、もとい標準偏差を採用したものを
資本市場線
といいますが、ここでは思いっきりスルーします。
さて、冒頭の表に戻ります。

ここで、以下の条件の場合の個別資産HNの期待収益率を求めてみましょう。
市場ポートフォリオの期待収益率が6%
個別資産HNのベータが1.3
無リスク資産の期待収益率が2%
「市場均衡関係式」というのがあって、それによると、
E(Ri)=Rf+(E〔RM〕-Rf)×β
だそうです。ちなみに、
- E(Ri):資産iの期待収益率
- Rf:無リスク資産の期待収益率
- 〔RM〕市場ポートフォリオの期待収益率
- β:資産iのベータ
うーん、よーくみればなんとなくわかるんだけど、
6月までには忘れてる。
そこで、グラフを見ながら思いました。
これって、要するに一次関数のグラフだから、
Y=AX+B
だよね?
つまり、式を覚えるより、グラフを書いて数字を入れて、計算すれば式忘れてても答えは出せます。出せるはずだ。
やってみましょう。

赤の数字が今回の問題で与えられている数字です。
まず、無リスク資産の期待収益率が2%ですから、切片(Y=AX+BのBのこと)は2です。つまり、
Y=AX+2
問題はAXのAですが、これは直線の傾きですね。そこで、直角三角形を書いてみましょう。

直線の傾きは
=4
意外とあっさり出ました。
しかもこの求め方だと、分母は必ず1になりますので、単純に市場ポートフォリオの期待収益率から無リスク資産の期待収益率を引けば傾きは出ます。
よって、今回の問題では
Y=4X+2
ということになります。
あとは、Xに1.3を入れるだけ。
Y=4×1.3+2=7.2
となり、個別資産HNの期待収益率は7.2%となります。
まあ、やってることはおんなじで、グラフを書いて式をすっきりさせただけなんですが、試験会場で式がとんじゃっても、頭の中が整理できるので、落ち着いて計算ができるというのが最大のメリットです。
まとめ
証券市場線とベータが出てきたら、グラフを書いてみる。
実は、「ジェンセンのアルファ」も、グラフを書くと結構あっさり求められます。
次回はそれをお伝えしたいと思います。